多维动态规划

编辑距离

主要是找到通项公式：使用dp[i][j]表示word1[:i]到word2[:j]需要使用的最少操作数，那么对应的通项公式如下：

$$ dp[i][j] = \left\{\begin{matrix} dp[i-1][j-1] & if\,\,\,\,word1[i] = word2[j]\\ min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) & if\,\,\,\,word1[i] != word2[j] \end{matrix}\right. $$

其次是初始化，对于dp[0][j]表示word1[:0]到word2[:j]需要使用的最少操作数，即dp[0][j]=j，dp[i][0]同理
使用python实现：

def minDistance(word1,word2):
    m = len(word1)
    n = len(word2)
    # 初始化
    dp = []
    for i in range(m+1):
        dp.append([0]*(n+1))
    for i in range(m+1):
        dp[i][0] = i
    for j in range(n+1):
        dp[0][j] = j
    for i in range(m):
        for j in range(n):
            if word1[i] == word2[j]:
                dp[i+1][j+1] = dp[i][j]
            else:
                dp[i+1][j+1] = min(dp[i+1][j],dp[i][j+1],dp[i][j]) + 1
    return dp[m][n]

最大正方形

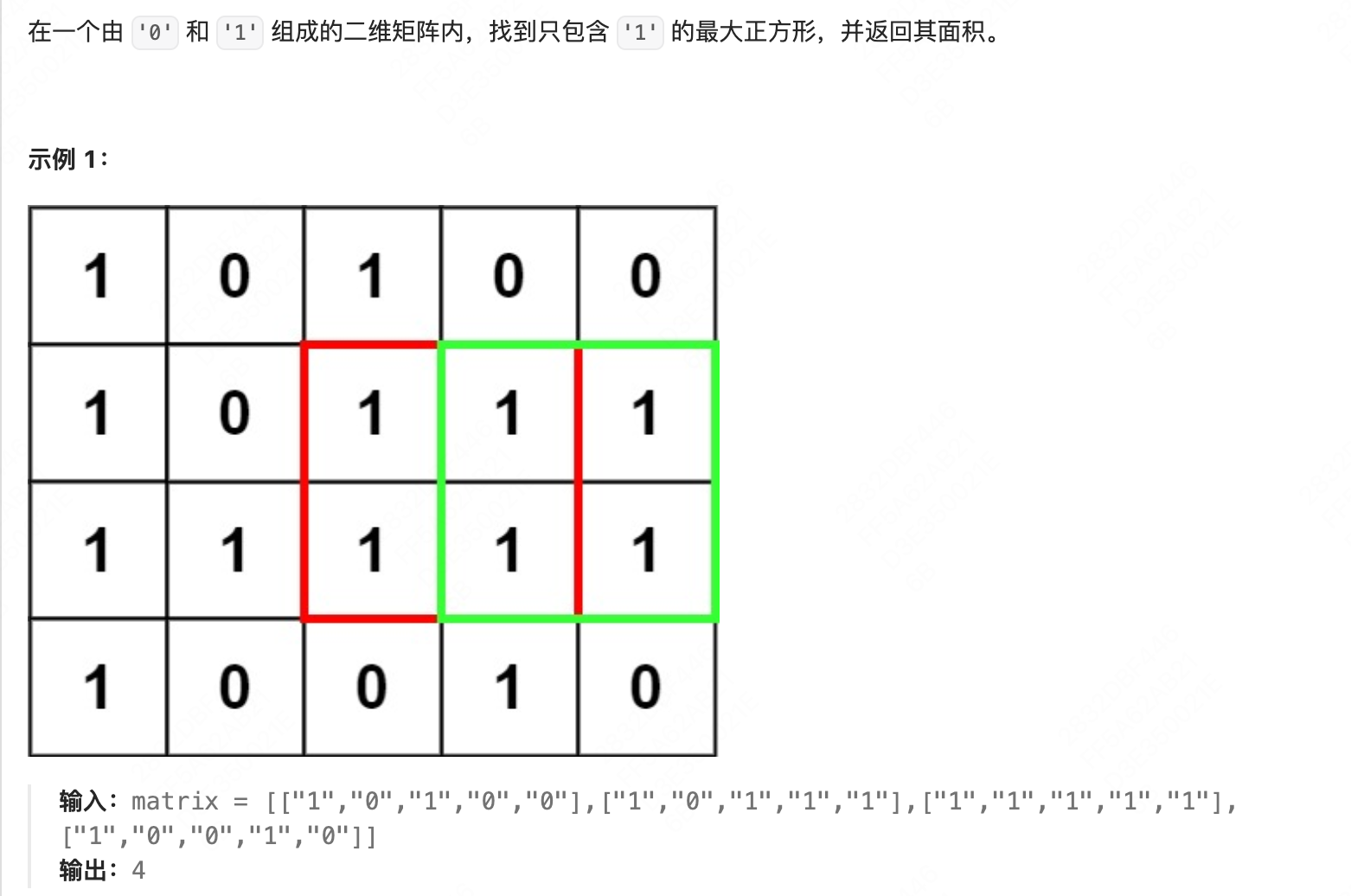
因为是正方形，题目变得简单，使用dp[i][j]表示以[i,j]为正方形的右下脚元素对应的最大正方形，如果右下角值为1，则最大的正方形等于左边dp[i][j-1]、上面dp[i-1][j]、中间dp[i-1][j-1]对应的最小值，即

$$ dp[i][j] = \left\{\begin{matrix} 0 & if\,\,\,\,matrix[i][j] = 0\\ min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) & if\,\,\,\,matrix[i][j] = 1 \end{matrix}\right. $$

上面那个通项公式绘制一个图就比较好理解了，借用leetcode上的解题图：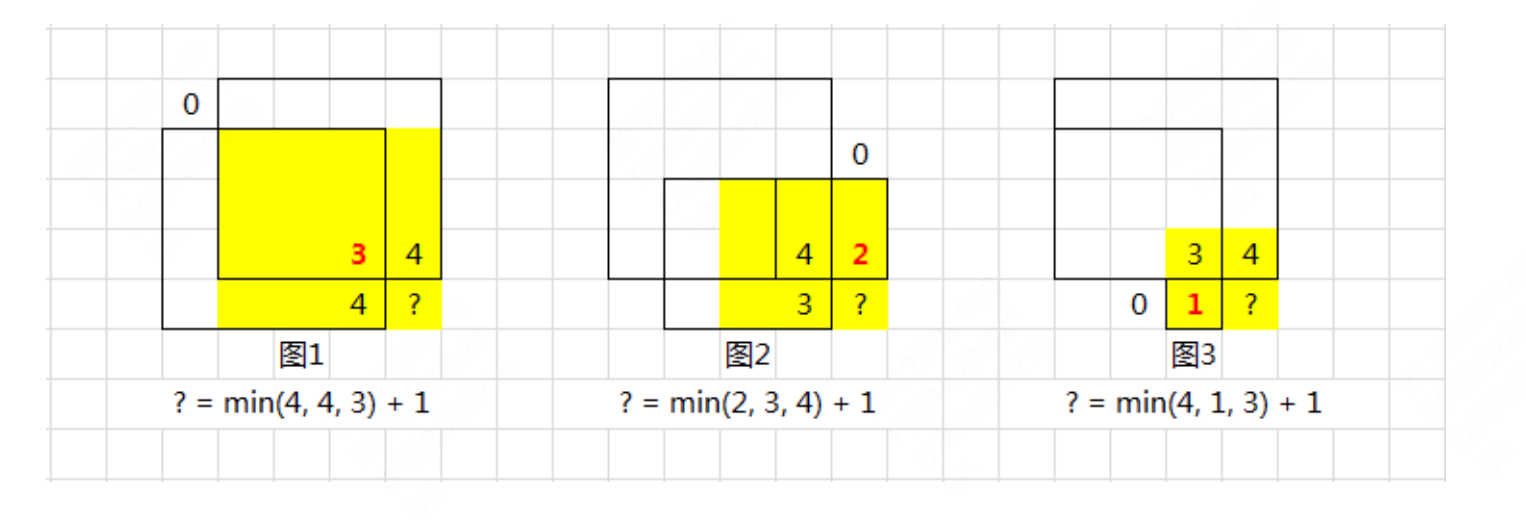

黄色部分是最大的正方形，图1所示，左边的最大正方形是4，中间的是3，上边的是4，则最大的是三者最小值3+1，图2所示，左边的是3，中间的是4，上边的是2，则最大的是三者最小值2+1

最小路径和

这种类型的题目很简单，因为通项公式很明显，用dp[i][j]表示从左上角到位置[i,j]路径值最短，则通项公式为：

$$ dp[i][j] = min(dp[i][j-1],dp[i-1][j]) + grid[i][j] $$

主要需要注意的是dp的初始化，[0,0]处的值是确定的，[0,j],[i,0]位置的值是确定的
使用python实现：

def minPathSum(self, grid: List[List[int]]) -> int:
    dp = []
    for i in range(len(grid)):
        dp.append([0]*len(grid[0]))
    dp[0][0] = grid[0][0]
    for i in range(1,len(grid)):
        dp[i][0] = dp[i-1][0] + grid[i][0]
    for j in range(1,len(grid[0])):
        dp[0][j] = dp[0][j-1] + grid[0][j]
    for i in range(1,len(grid)):
        for j in range(1,len(grid[i])):
            dp[i][j] = min(dp[i][j-1],dp[i-1][j]) + grid[i][j]
    return dp[-1][-1]

一维动态规划

最长递增子序列

用dp[i]表示以第i个位置为终点对应的最长递增子序列，则该值等于前面所有满足条件的最大dp值，即通项公式为：

$$ dp[i] = (\max_{j,nums[j]<nums[i]}^idp[j]) + 1 $$

最后还需要转换一下，因为dp[i]表示的是以第i个位置为终点对应的最长递增子序列，题目是需要的是任意一个子序列，并不是非得包括最后一个元素，用python实现如下：

def lengthOfLIS(self, nums: List[int]) -> int:
    ret = 0
    dp = [0]*len(nums)
    for i in range(len(nums)):
        max_value = 1
        for j in range(i):
            if nums[j]<nums[i]:
                max_value = max(max_value,dp[j]+1)
        dp[i] = max_value
        ret = max(ret,max_value)
    return ret

零钱兑换

常规dp解法，dp[i]表示总金额为i时需要的最少硬币数，等于前面满足条件的最小dp值，即通项公式为：

$$ dp[i] = (\min_{c_k}^{coins}dp[i-c_k]) + 1 $$

注意无法组合的处理，使用python实现如下：

def coinChange(self, coins: List[int], amount: int) -> int:
    dp = [0]*(amount+1)
    for i in range(1,amount+1):
        cur_num = amount+1
        for k in coins:
            if i-k>=0:
                cur_num = min(cur_num,dp[i-k]+1)
        dp[i] = cur_num
    return dp[amount] if dp[amount]<=amount else -1

单词拆分

定义dp[i]为s[:i]是否可以由wordDDict组成，则需遍历满足条件（这个条件就是s[:i]的尾部可以由wordDDict中的某个词等价）的子串是否可以由wordDDict组成，用python实现如下：

def wordBreak(self, s: str, wordDict: List[str]) -> bool:
    dp = [False]*(len(s)+1)
    dp[0] = True
    for i in range(len(s)):
        states = False
        for w in wordDict:
            w_length = len(w)
            if i+1-w_length>=0 and s[i+1-w_length:i+1] == w:
                states = states or dp[i+1-w_length]
        dp[i+1] = states
    return dp[-1]

打家劫舍

这个题稍微有点不同，需要用到两个一维数组，比如如果用dp[i]表示当前位置能偷到的最大值，由于题目中提到不能连着偷，dp数组中没法知道i-1个位置是否偷过，因此一个位置应该有两个状态，该位置被偷的情况下能偷的最大值，该位置不被偷的情况下能偷的最大值，最后取这两个的最大值，对应的通项公式如下：

$$ dp[0][i] = max(dp[1][i-1],dp[0][i-1]) \\ dp[1][i] = dp[0][i-1] + nums[i] $$

用python实现：

def rob(self, nums: List[int]) -> int:
    dp = [[0]*len(nums),[0]*len(nums)]
    dp[0][0] = 0
    dp[1][0] = nums[0]
    for i in range(1,len(nums)):
        dp[0][i] = max(dp[1][i-1],dp[0][i-1])
        dp[1][i] = dp[0][i-1] + nums[i]
    return max(dp[0][-1],dp[1][-1])