柱状图中最大的矩形

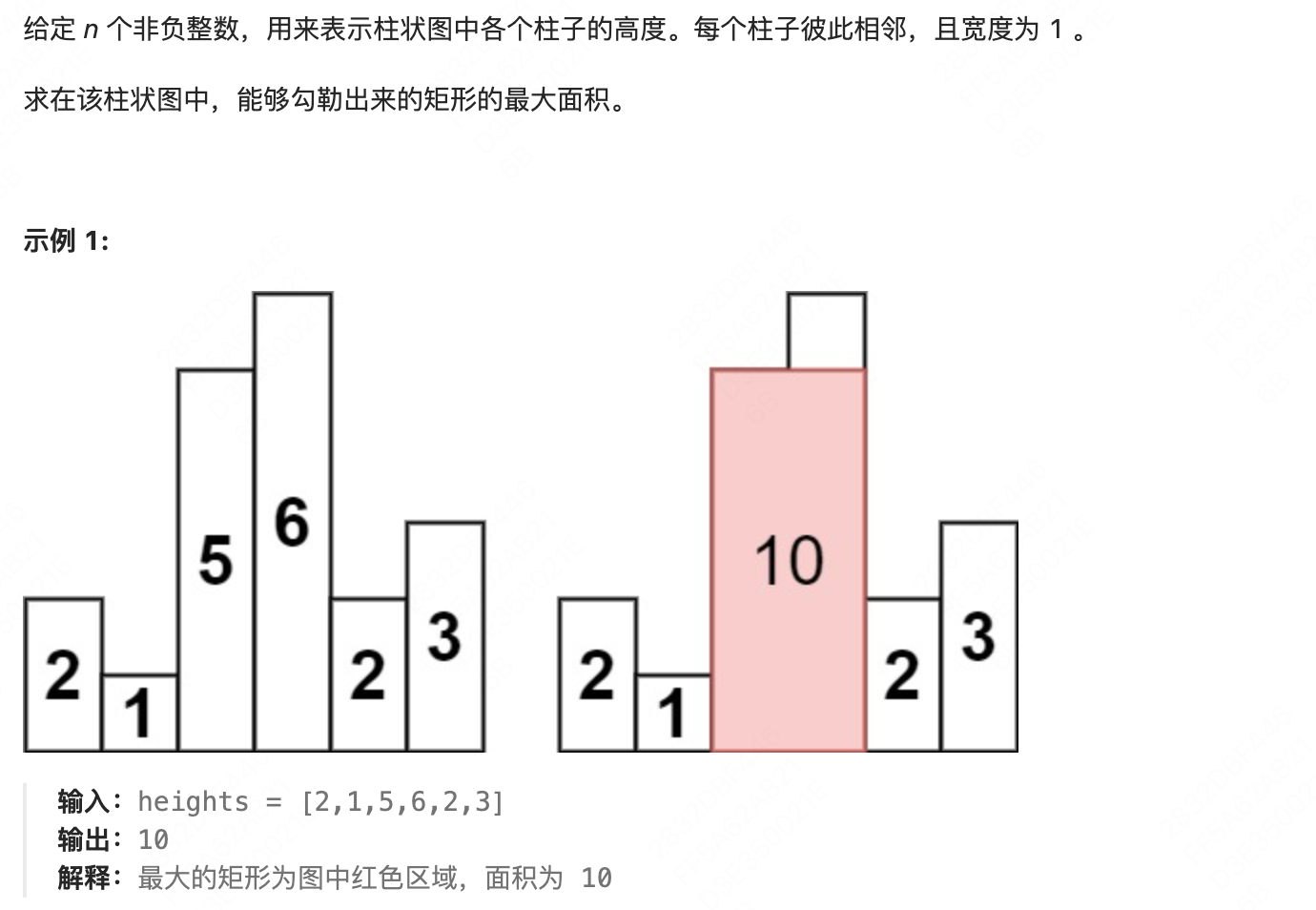
简单理解，对于每个高度，找到其对应的最大矩阵，然后从这些矩阵中找出最大的矩阵，则为柱状图中最大的矩阵，那给定一个高度，如何找到其对应的最大矩阵呢，即往左往右遍历，需要保证遍历的每一个高度都要大于等于该高度，直到不满足停止，这样形成的矩阵是该高度对应的最大矩阵，即：找到左边最近的小于该高度的位置 和 找到右边最近的小于该高度的位置，这需要借助单调栈

以下用python代码实现：

def largestRectangleArea(heights):
    stack = []
    n = len(heights)
    right_list = [n]*n
    left_list = [0]*n
    # 找到i位置右边能延伸的最大范围
    for i in range(n):
        while len(stack) > 0 and heigths[stack[-1]] > heights[i]:
            right_list[stack[-1]] = i
            stack = stack[:-1]
        stack.append(i)
    # 找到i位置左边能延伸的最大范围
    stack = []
    i = n-1
    while i>=0:
        while len(stack) > 0 and heigths[stack[-1]] > heights[i]:
            left_list[stack[-1]] = i + 1
            stack = stack[:-1]
        stack.append(i)
    # 计算最大的矩阵
    max_value = 0
    for i in range(n):
        max_value = max(max_value,(right_list[i]-left_list[i])*heights[i])
    return max_value

上面的写法是为了更好的理解，其实也可以简化，左右范围一起算：

def largestRectangleArea(heights):
    n = len(heights)
    stack = []
    left = [0]*n
    right = [n]*n
    for i in range(n):
        while len(stack)>0 and heights[stack[-1]] > heights[i]:
            right[stack[-1]] = i
            stack = stack[:-1]
        # 当前i的最远左边是0或者单调栈中的栈顶元素对应的位置
        left[i] = stack[-1] if len(stack)>0 else -1
    max_value = max([heights[i]*(right[i]-left[i]-1) for i in range(n)])
    return max_value

接雨水

对于每个位置，需要找到其左边最大值和右边最大值，然后取这两个值对应的最小值，减去该位置的高度，即为该位置能够接的水量，相对余上面一题来说更简单，下面用python实现：

def trap(height):
    left = [0]*len(height)
    right = [0]*len(height)
    cur = 0
    for i in range(len(height)):
        cur = max(cur,height[i])
        left[i] = cur
    cur = 0
    for i in range(len(height)-1,-1,-1):
        cur = max(cur,height[i])
        right[i] = cur
    s = 0
    for i in range(len(height)):
        s += min(left[i],right[i]) - height[i]
    return s